Cómo calcular el desplazamiento de fase

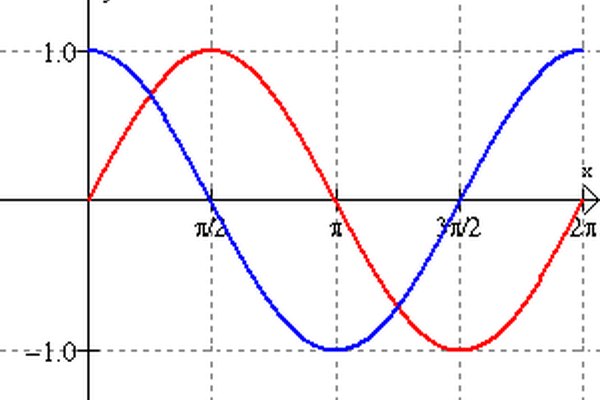
La fase de una función curva indica su desplazamiento horizontal a una curva de seno. Una función curva simplificada es una función que tiene la forma y = SenA(2Pi[fx] + ?) donde A es la amplitud, f es la frecuencia y ? es la fase. Nota que esta forma simplificada no da un desplazamiento o rotación vertical de la función seno. La ilustración que sigue muestra que la función coseno, en azul, alcanza su altura máxima cuando x = 0 mientras que la función seno, en rojo, alcanza su altura máxima cuando x = Pi/2. La curva del coseno por lo tanto tiene una fase de Pi/2.

Mide el desplazamiento horizontal entre dos funciones curvas graficándolas. Un desplazamiento a la derecha indica una fase positiva y uno a la izquierda indica una fase negativa.

Determina el desplazamiento de fase entre la función coseno y la función seno. Usa la ecuación de identidad trigonométrica cos(x) = sen(x+Pi/2) para demostrar que se puede obtener la función coseno desplazando la curva de seno Pi/2 hacia la izquierda. La función coseno, es por lo tanto la función seno con un desplazamiento de fase de -Pi/2.

Generaliza la función curva del seno con la ecuación sinusoidal y = senA(B[x - C]) + D. En esta ecuación, la amplitud de la curva es A, el factor de expansión es B, el desplazamiento de fase es C y el desplazamiento de amplitud es D.

Expresa una función curva con la ecuación y = senA(B[x - C]) para determinar su desplazamiento de fase C. Por ejemplo, para la función cos(x) = sen(x+Pi/2) = sen(x - [-Pi/2]), tenemos que C = -Pi/2. Por lo tanto, el desplazamiento de la fase de la función seno en -Pi/2 producirá la función coseno.

Calcula el desplazamiento de fase de la función y = sen(2x - Pi/2). Esta función es igual a y = sen(2[x - Pi/4]) donde A = 1, B = 2, C = Pi/4 y D = 0. El desplazamiento de fase para y = sen(2x - Pi/2) es por lo tanto Pi/4.