¿Qué es delta en matemáticas?

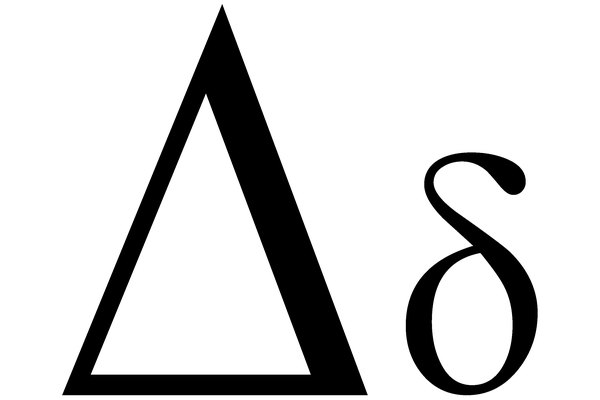
Con el desarrollo de las matemáticas y otras ciencias durante los últimos 500 años fue haciéndose cada vez más necesario actualizar la nomenclatura de muchos términos y buscar formas de representar de una manera fácil y universal los números, funciones, sistemas y ecuaciones que fueran saliendo a la luz.

Tomando en cuenta el papel de los griegos en el nacimiento de las matemáticas y otras ciencias, la mayoría de los estudiosos apoyaron usar el alfabeto griego como un método sencillo para dar nomenclatura a estos símbolos y conceptos.

Lee también: Cómo calcular un porcentaje delta

De esta manera, la letra Delta, que en mayúscula se escribe (Δ) y en minúscula (δ) fue adoptada para simbolizar diferentes conceptos. La letra Delta tiene también un valor numérico de 4 y se corresponde con la letra “D” del alfabeto latino en el que se basan la mayoría de los idiomas occidentales hoy en día.

Vamos a repasar los usos que recibe la letra Delta dentro de varias de las ramas del saber humano.

La letra Delta en matemáticas

En las matemáticas y las ciencias aplicadas, la letra Delta en mayúscula (Δ) fue adoptada como una forma de expresar que una variable está sometida a un "cambio".

Por ejemplo, si la variable "x" representa el movimiento de un objeto, entonces, "Δx" significa "el cambio en el movimiento" de ese objeto.

Por su parte, en matemática avanzada se usa la letra delta minúscula (δ) para definir una función denominada delta de Kronecker.

La delta de Kronecker representa una relación entre dos variables integrales, la cual es 1 si las dos variables son iguales y 0 si no lo son.

¿Qué significado tiene la letra Delta en álgebra?

En álgebra, la Delta mayúscula (Δ) a menudo representa el discriminante de una ecuación polinómica, usualmente una ecuación de segundo grado.

Un discriminante da información acerca de las raíces de la ecuación cuadrática: dependiendo del valor de Δ, una ecuación cuadrática puede tener dos raíces reales, una raíz real o dos raíces complejas.

Dada la ecuación cuadrática ax² + bx + c, por ejemplo, el discriminante de la ecuación será igual a b² - 4ac, y se denota como Δ = b² – 4ac.

Uso de Delta para definir ángulos en geometría

En geometría, la delta minúscula (δ) puede representar un ángulo en cualquier forma geométrica. Esto se debe a que la geometría tiene sus raíces en la obra de Euclides en la antigua Grecia, y los matemáticos después denotaron los ángulos con letras griegas.

Debido a que las letras representan simplemente ángulos, el conocimiento del alfabeto griego y su orden no es necesario para entender su significado en este contexto.

¿Cómo se usa Delta en las derivadas parciales?

La derivada de una función es una medida de los cambios infinitesimales en una de sus variables y la letra romana "d" representa una derivada regular.

Por su parte, las derivadas parciales se diferencian de las derivadas regulares en que la función tiene múltiples variables, pero se considera sólo una variable: las otras variables permanecen fijas.

Las derivadas parciales se representan con una delta minúscula (δ), por lo que la derivada parcial de la función "f" se ve así: δf sobre δx.

¿Qué uso tiene Delta en ingeniería?

En la ingeniería la letra griega delta en mayúscula es usada para señalar diferencias entre entidades de variada índole.

Esto significa que se usa para definir la diferencia entre un valor final y un valor de inicio. Por ejemplo, supongamos que queremos señalar una “diferencia de presión”, para lo que usaríamos la expresión (∆P = Pf-Pi), que se calcularía de la resta entre el valor final y el valor inicial de una medida de presión.

Te puede interesar: Como factorizar polinomios más difíciles

También podemos usarla con otras variables como temperatura, altura, entropía, etc.

Esto se expresaría de la siguiente forma:

∆T= (Tf – Ti) diferencia de temperatura

∆S= (Sf – Si) diferencia de entropía

∆h= (hf – hi) diferencia de altura