Cómo saber cuando una fracción es mayor que otra

Puede que pienses que saber qué fracción es mayor a otra no es un tema relevante, pero puede llegar a serlo. Las fracciones son un tema elemental de la escuela y estarán presentes en nuestras vidas, en especial si se eligen carreras científicas.

Además, conocer cómo sumar, restar, comparar o convertir fracciones en números con decimales es necesario en el día a día, ya sea para entender una receta de cocina o ayudar a los niños con las tareas de comparación de fracciones en primaria.

¿Qué son las fracciones y para qué se usan?

Una fracción no es más que la demostración numérica de una parte con respecto a la unidad. Por ejemplo, 1/2 de litro de agua es la mitad de 1 litro o lo que es igual, 0,5 litros o 500 mililitros. Tal como puede verse, la fracción indica cuántas partes (numerador) hay en una unidad (denominador).

• El numerador es el número que está encima de la raya de la fracción y expresa cuántas partes se han seleccionado de un objeto al que llamaremos “equis”
• El denominador es el número indicado debajo de la raya de la fracción y expresa en cuántas partes iguales se dividió ese objeto

Podría interesarte: Cómo explicar las fracciones paso a paso

Veámoslo en un ejemplo. Supongamos que debemos repartir un pastel redondo a seis niños y queremos guardar dos pedazos para después. Para que nadie se disguste, cortamos el pastel en ocho partes iguales.

En este ejemplo, el pastel es el objeto equis; las ocho partes iguales el denominador y la cantidad de porciones que serán repartidas, el numerador. Si quisiéramos expresar en fracciones cuántas porciones de pastel se repartieron y cuántas se almacenaron, sería:

¿Cómo determinar qué fracción es mayor que la otra?Como puede observarse, ambas fracciones tienen los mismos denominadores, es decir, que pertenecen a una unidad que fue dividida en ocho pedazos iguales. Si quisiéramos decir qué fracción es mayor en este ejemplo, sería la de seis octavos (6/8). Pero, ¿qué pasaría si las fracciones tuvieran denominadores diferentes?

Hay varias formas de saber qué fracción es menor que otra o viceversa, pero el método más fácil, simple y rápido de hacer es a través de la multiplicación cruzada.

Podría interesarte: Cómo restar fracciones de números enteros

Supongamos que tenemos dos fracciones y deseamos saber cuál es mayor

Lo que debes hacer es multiplicar el numerador de la primera por el denominador de la segunda y luego, el denominador de la primera por el numerador de la segunda, así:

3 x 10 = 30

4 x 6 = 24

Anota el primer resultado al lado de la primera fracción, y el segundo junto a la restante.

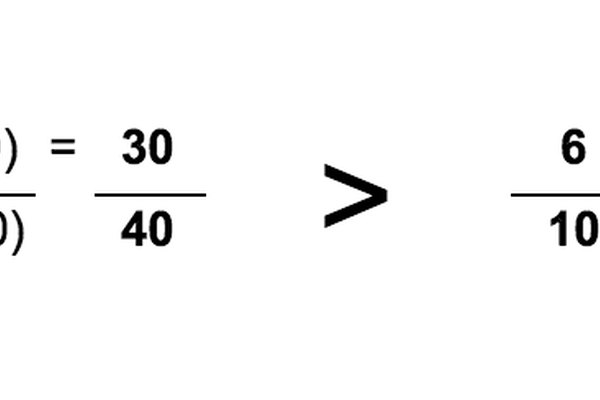
Como el número 30 es mayor a 24, 3/4 es mayor que 6/10. Pero deberás representarlo en forma de fracción. Hasta ahora, tienes dos numeradores, 30 y 24. Te hace falta un mismo denominador.

Para calcularlo, multiplica los denominadores entre sí (4 x 10= 40) y coloca la fracción con el común denominador al lado para demostrar por qué una es mayor que la otra.

También puedes intentar hacerlo buscando el mínimo común denominador. Aprender este método puede resultarte bastante útil, en especial si tienes varias fracciones que comparar.Método alterno: mínimo común denominador

Para hacerlo, deberás descomponer los denominadores en sus factores primos. Esto se realiza buscando la mitad del denominador o dividiéndolo entre 2 hasta que el número que quede sea igual a uno.

Veámoslo gráficamente:

Sigue leyendo: Cómo hallar el mínimo común múltiplo de forma sencilla y ver algunas de sus aplicaciones


También puedes encontrarlo haciendo una lista de los múltiplos del denominador:

• En el caso de 4: 4, 8, 12, 16, 20...
• En el caso de 10: 10, 20, 30…

Como puedes ver, el número 20 se repite en ambas listas. Este será tu denominador común.

Ahora, basta con dividir el denominador común entre los denominadores de cada fracción y multiplicar el producto, tanto por el numerador como por el denominador, así:

En el caso de 3/4: 20 entre 4 = 5

En el caso de 6/10: 20 entre 10 = 2

Por tanto:

Si te fijas, si multiplicas por 2 cada una de estas fracciones, tendrás el mismo resultado que con el método de la multiplicación cruzada, lo que te demuestra que la primera técnica arrojó un resultado correcto, solo que no con el mínimo común denominador.

Fácil, ¿no?