Cómo resolver problemas básicos de probabilidad con un mazo de cartas

El artículo 3 en una serie de artículos independientes sobre probabilidad básica. Un tema común en la probabilidad de introducción es la solución de problemas con un mazo de cartas estándar. Este artículo muestra los pasos para solucionar los tipos más comunes de preguntas básicas sobre este tema.

Para todos los problemas de este tipo, hay algunos puntos importantes que se aplican. En primer lugar, el problema probablemente se referirá a un mazo de cartas. Esto significa que no hay trucos implicados. El problema supone un mazo de cartas, no "apilado", mezcladas al azar, extrayendo las cartas al azar.

Algunos estudiantes afirman que las cuestiones de esta naturaleza son injustas, especialmente si se criaron en una cultura que no juega a los juegos utilizando lo que llamamos comúnmente como un mazo de cartas. Si bien este puede ser el caso, no es difícil de aprender los hechos acerca de un mazo de cartas que supones conocer.

Un mazo de cartas contiene 52 cartas diferentes. Contiene cartas de 13 rangos diferentes, que van desde el As (esencialmente 1) hasta el 10, seguido por Jack, Reina, Rey, que podrías pensar que son el 11, 12 y 13. En cada rango hay cartas de cuatro palos: un corazón, una pica, un diamante, y una pala. Los corazones y los diamantes son rojas, y los picos y las palas son de color negro. Hay 4 cartas de cada rango, y 13 cartas de cada palo. No hay comodines. Eso es todo lo que necesitas saber para responder a cualquier problema relacionado con un mazo de cartas.

Aquí puedes ver un problema simple: "Una persona agarra una carta de un mazo de cartas estándar, y es la Reina de Corazones La carta se pone nuevamente en el mazo, y se vuelven a barajar. ¿Cuáles son las posibilidades de agarrar la Dama de Picas en el próximo sorteo?". En primer lugar, la palabra "reemplazar" en este contexto significa "colocar nuevamente".

Esto es realmente una pregunta con trampa. El hecho de que la Reina de Corazones se extrajo ​​en el primer sorteo no tiene nada que ver con el segundo sorteo, ya que se devuelve a la baraja, y se baraja el mazo nuevamente. El mazo no tiene memoria. Es incorrecto decir que la Reina de Corazones está de "suerte", por lo que es más probable que salga de nuevo, al igual que es incorrecto decir que la Reina de Corazones tenga menos probabilidad de salir nuevamente, porque las otras cartas están "atrasadas". La respuesta a la pregunta no es más que 1/52.

Aquí puedes ver otro problema típico con algunos de los términos estándar omitidos por brevedad: "¿Cuáles son las probabilidades de sacar una carta roja?". Hay 2 cartas de figuras rojas de 13 cartas cada una, así que la respuesta es 26/52 que probablemente se reduciría a 1/2". ¿Cuáles son las posibilidades de sacar un siete?". Hay cuatro sietes de 52 cartas, lo que nos da 4/52 que probablemente se reduciría a 1/13". ¿Cuáles son las posibilidades de sacar una carta de picas?" Hay 13 picas de 52, lo que nos da 13/52 que probablemente se reduciría a 1/13.

Debes estar atento a las preguntas capciosas: "¿Cuáles son las posibilidades de sacar una carta verde?". La respuesta es 0. No hay ninguna carta verde. "¿Cuáles son las posibilidades de sacar una carta ya sea de color roja o de color negro?". La respuesta es 52/52, que es igual a 1, o equivalente a 100%. Cada carta de la baraja es una o la otra.

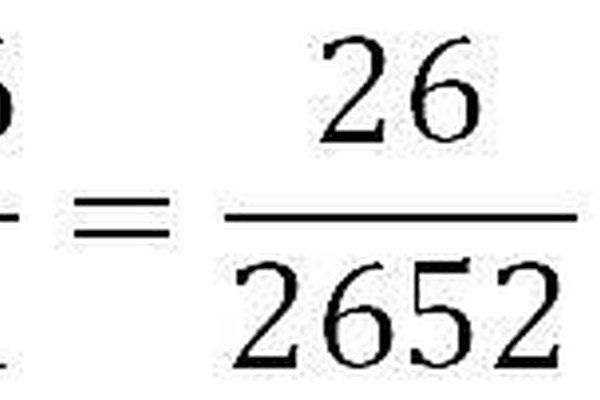
Aquí puedes ver un problema que es un poco más complicado: "Dos cartas se extraen de un mazo sin reemplazo ¿Cuáles son las posibilidades de sacar el nueve de picas seguido por una tarjeta roja?". En primer lugar, toma nota del hecho de que no vas a colocar nuevamente la primera carta en el mazo después de extraerla de éste. Las posibilidades de sacar el nueve de picas en la primera extracción es 1/52. Ahora que la tarjeta se ha sacado, nos quedan 51 cartas en el mazo. Las posibilidades de sacar una tarjeta roja de las cartas que quedan son 26/51. Todavía hay 26 tarjetas en el mazo, ya que el nueve de picas no era una de estas.

Este problema implica una condición "y", y para estos problemas se deben multiplicar las probabilidades individuales. Debemos multiplicar 1/52 veces 26/51, lo que nos da 26/2652, que probablemente se reduciría a 1/102.

Aquí hay otro problema típico: "Dos cartas se extraen de un mazo de barajas estándar con reemplazo, y barajándolas en cada oportunidad, ¿cuáles son las posibilidades de sacar un tres en la primera extracción, y un diamante en la segunda extracción?". Toma nota del hecho de que se trata de un escenario de sustitución. Las posibilidades de sacar un tres en la primera extracción es de 4/52. Las posibilidades de sacar un diamante en la segunda extracción es de 13/52. Cada extracción no tiene nada que ver con la anterior, ya que cada una comenzó a partir de un mazo completo de barajas. Multiplica 4/52 veces 13/52 para obtener 52/2704, que se reduce a 1/52.

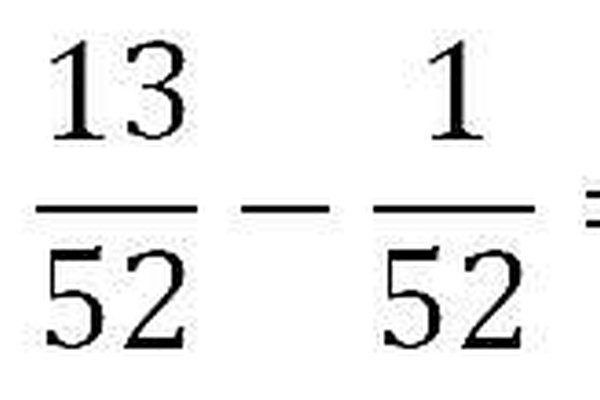
Aquí puedes ver un último problema típico que puede ser un poco complicado. "¿Cuáles son las posibilidades de extraer un cinco o una carta de diamantes?". Se trata de una situación con una "o", lo que significa que tenemos que añadir (no multiplicar) las probabilidades involucradas. Las posibilidades de extraer un cinco son de 4/52. Las posibilidades de extraer una carta de diamantes son 13/52. Muchos estudiantes solo tienen que añadir las dos fracciones en conjunto para obtener 17/52, pero esto en realidad es un error. El problema es que hemos contado el cinco de diamantes dos veces, una como un cinco, y otra vez como un diamante. Tenemos que restar uno de esos momentos, para poder contarlo solo una vez, así que terminamos con 16/52, que es la respuesta correcta.

Otra forma de verlo es pensar que hay 13 cartas de diamantes en el mazo, y luego solo tenemos que contar los tres cincos que no son de diamantes. Eso nos da 16 cartas de 52 posibles.

Los estudiantes deben asegurarse de sentirse cómodos trabajando con los conceptos básicos de probabilidad mencionados en este artículo, ya que los verán con bastante frecuencia.